堆：

• 堆是一种完全二叉树，复习一下完全二叉树的定义，完全二叉树的形式是指除了最后一层之外，其他所有层的结点都是满的，而最后一层的所有结点都靠左边。
• 若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

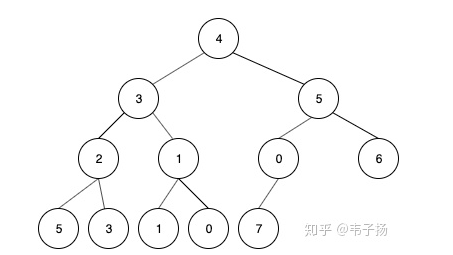
完全二叉树：对于任意一个父节点的序号n来说（这里n从0算），它的子节点的序号一定是2n+1,2n+2，因此我们可以直接用数组来表示一个堆。

堆的创建：

class Heap{
    constructor(){
        this.array = []
        this.length = 0
    }
}

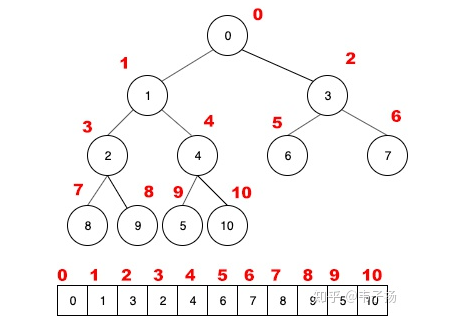
大顶堆/最大堆：

对于任意一个父节点来说，其子节点都小于这个父节点

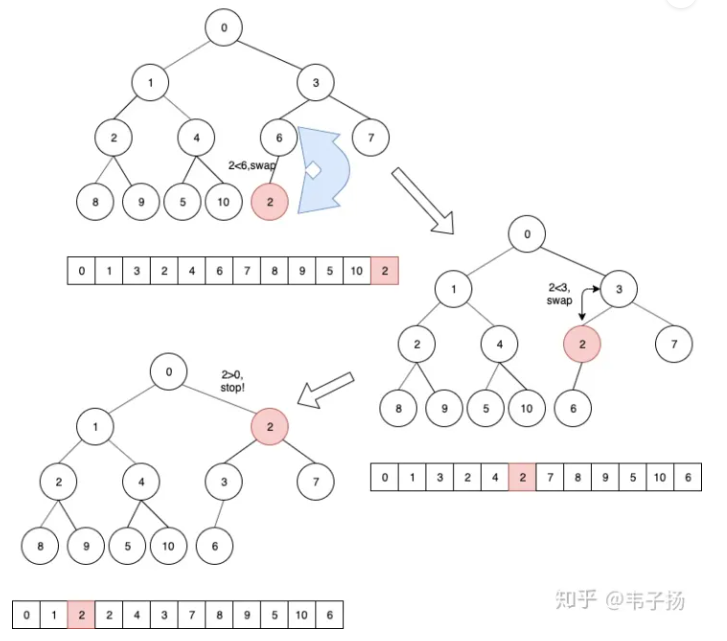
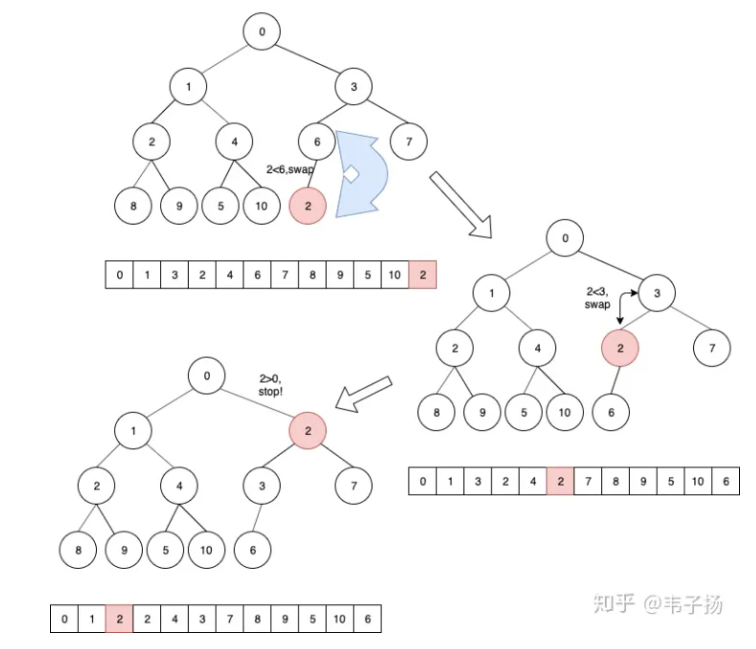
最大堆的插入：

• 当一个元素要插入时，先放到堆尾，根据堆的特性，对位置进行调整。
• 父节点要大于直接点，找到插入节点的父节点，比父节点值大则交换位置，否则插入成功
• 交换后，继续检测该节点与现在父节点的大小，如果大则交换位置，一直上浮到根节点

JavaScript实现：length可以用this.array.length替代

insert(x){
    this.array.push(x)
    if(this.array.length===0){
        return
    }
    let x_index = this.array.length-1
    let parent_index = x_index
    while(parent_index!==0){
        let parent_index = x_index%2===0?(x_index-2):(x_index-1)
        parent_index = parent_index/2
        if(this.array[parent_index]<x){
            this.array[x_index] = this.array[parent_index]
            this.array[parent_index] = x
        }else{
            break
        }
        x_index = parent_index
    }
    return
}
// 循环最大次数k即为树的深度：2^0+2^1+...+2^k = n 即k=logn 时间复杂度为O(logN)

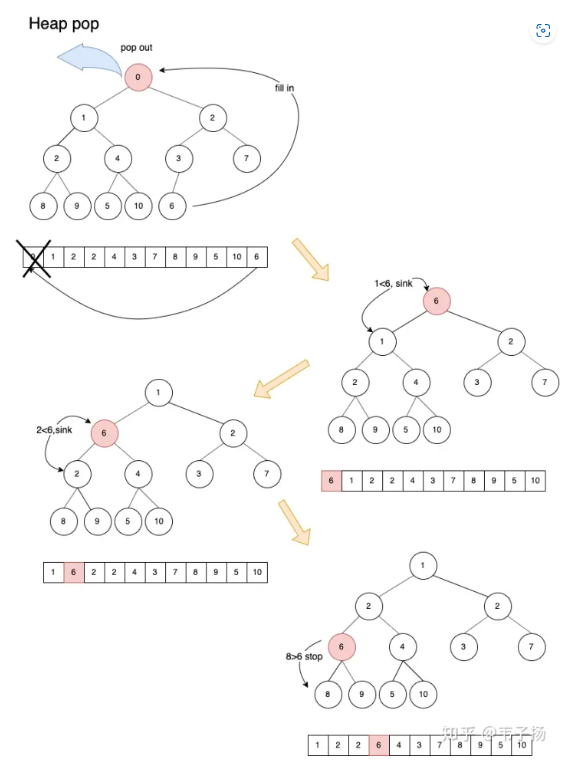
最大堆的删除

• 堆的删除一般是值删除堆顶元素，先删除堆顶元素
• 要保证堆一直为完全二叉树，不能直接拿子节点的较大值，而是将末尾元素拿到堆顶，再下沉
• 下沉即先比较该节点与左子节点，如果子节点更大，则交换，如果子节点更小，则与右节点比较
• 直至到最深层，或者比左右子节点都大

JavaScript实现：

pop(){
    this.array[0] = this.array[this.array.length-1]
    this.array.pop()
    let x_index = 0
    while(true){
        let left_index = 2 * x_index + 1
        let right_index = 2 * x_index + 2
        left_index = left_index>=this.array.length?x_index:left_index
        right_index = right_index>=this.array.length?x_index:right_index
        let large_child_index = this.array[x_index]<this.array[left_index]?left_index:x_index
        large_child_index = large_child_index!==x_index?large_child_index:(this.array[x_index]<this.array[right_index]?right_index:x_index)
        if(large_child_index===x_index) break
        let temp = this.array[x_index]
        this.array[x_index] = this.array[large_child_index]
        this.array[large_child_index] = temp
        x_index = large_child_index
    }

}
// 最大循环次数k即为树的深度 k = logn 时间复杂度为O(logN)

小顶堆/最小堆

插入与删除与最大堆类似

插入JavaScript实现：

insert(x){
    debugger
    this.array.push(x)
    if(this.array.length===0){
        return
    }
    let x_index = this.array.length-1
    let parent_index = x_index
    while(parent_index!==0){
        let parent_index = x_index%2===0?(x_index-2):(x_index-1)
        parent_index = parent_index/2
        if(this.array[parent_index]>x){
            this.array[x_index] = this.array[parent_index]
            this.array[parent_index] = x
        }else{
            break
        }
        x_index = parent_index
    }
    return
}

删除JavaScript实现：

pop(){
    debugger
    this.array[0] = this.array[this.array.length-1]
    this.array.pop()
    let x_index = 0
    while(true){
        let left_index = 2 * x_index + 1
        let right_index = 2 * x_index + 2
        left_index = left_index>=this.array.length?x_index:left_index
        right_index = right_index>=this.array.length?x_index:right_index
        let small_child_index = this.array[x_index]>this.array[left_index]?left_index:x_index
        small_child_index = small_child_index!==x_index?small_child_index:(this.array[x_index]>this.array[right_index]?right_index:x_index)
        if(small_child_index===x_index) break
        let temp = this.array[x_index]
        this.array[x_index] = this.array[small_child_index]
        this.array[small_child_index] = temp
        x_index = small_child_index
    }

}

解决前K个高频元素/低频元素题

LeetCode链接

给定一个非空的整数数组，返回其中出现频率前 k 高的元素。

示例 1:

• 输入: nums = [1,1,1,2,2,3], k = 2
• 输出: [1,2]

示例 2:

• 输入: nums = [1], k = 1
• 输出: [1]

提示：

• 你可以假设给定的 k 总是合理的，且 1 ≤ k ≤ 数组中不相同的元素的个数。
• 你的算法的时间复杂度必须优于 $O(n \log n)$ , n 是数组的大小。
• 题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的。
• 你可以按任意顺序返回答案。

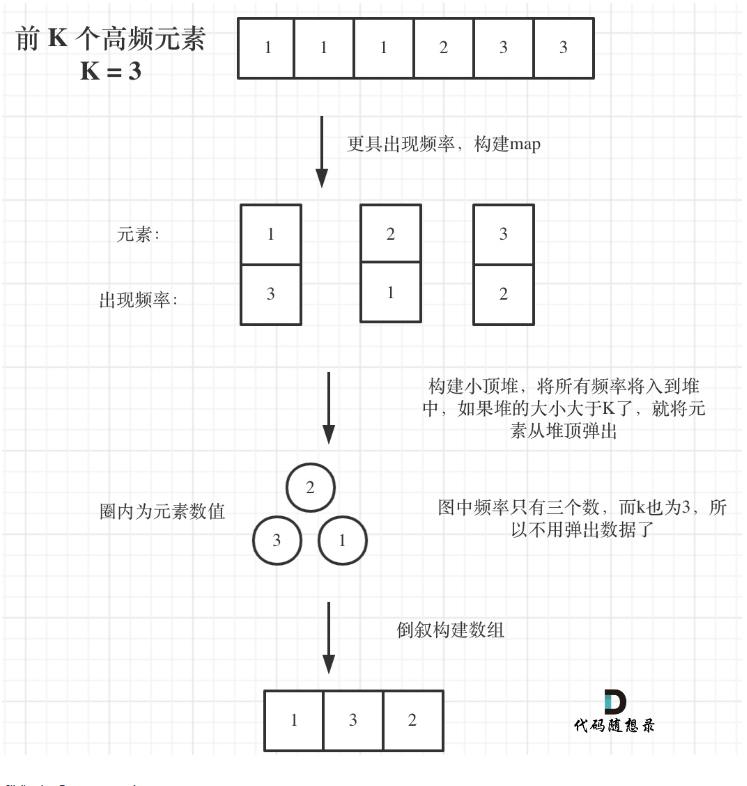
步骤：

• 获取到每个数据出现的频率，使用哈希表，这里可以用map，key是数字，value是次数
• 对频率排序
• 找出前K个高频元素

注：

• 如果使用快速排序的时间复杂度为O(n)
• 仅维护大小为K的小顶堆，小顶堆的堆顶始终是最小值，如果堆长度小于K则继续往队礼添加，如果长度大于K则弹出堆顶的最小值

// js 没有堆 需要自己构造
class Heap {
    constructor(compareFn) {
        this.compareFn = compareFn;
        this.queue = [];
    }

    // 添加
    push(item) {
        // 推入元素
        this.queue.push(item);

        // 上浮
        let index = this.size() - 1; // 记录推入元素下标
        let parent = Math.floor((index - 1) / 2); // 记录父节点下标

        while (parent >= 0 && this.compare(parent, index) > 0) { // 注意compare参数顺序
            [this.queue[index], this.queue[parent]] = [this.queue[parent], this.queue[index]];

            // 更新下标
            index = parent;
            parent = Math.floor((index - 1) / 2);
        }
    }

    // 获取堆顶元素并移除
    pop() {
        // 堆顶元素
        const out = this.queue[0];

        // 移除堆顶元素 填入最后一个元素
        this.queue[0] = this.queue.pop();

        // 下沉
        let index = 0; // 记录下沉元素下标
        let left = 1; // left 是左子节点下标 left + 1 则是右子节点下标
        let searchChild = this.compare(left, left + 1) > 0 ? left + 1 : left;

        while (searchChild !== undefined && this.compare(index, searchChild) > 0) { // 注意compare参数顺序
            [this.queue[index], this.queue[searchChild]] = [this.queue[searchChild], this.queue[index]];

            // 更新下标
            index = searchChild;
            left = 2 * index + 1;
            searchChild = this.compare(left, left + 1) > 0 ? left + 1 : left;
        }

        return out;
    }

    size() {
        return this.queue.length;
    }

    // 使用传入的 compareFn 比较两个位置的元素
    compare(index1, index2) {
        // 处理下标越界问题
        if (this.queue[index1] === undefined) return 1;
        if (this.queue[index2] === undefined) return -1;

        return this.compareFn(this.queue[index1], this.queue[index2]);
    }

}

const topKFrequent = function (nums, k) {
    const map = new Map();

    for (const num of nums) {
        map.set(num, (map.get(num) || 0) + 1);
    }

    // 创建小顶堆
    const heap= new Heap((a, b) => a[1] - b[1]);

    // entry 是一个长度为2的数组，0位置存储key，1位置存储value
    for (const entry of map.entries()) {
        heap.push(entry);

        if (heap.size() > k) {
            heap.pop();
        }
    }

    // return heap.queue.map(e => e[0]);

    const res = [];

    for (let i = heap.size() - 1; i >= 0; i--) {
        res[i] = heap.pop()[0];
    }

    return res;
};

由于key和value是要绑定的，所以元素不能是简单的数组，而应该是包含key和value的二维数组，同时为了使得代码重用，将比较函数抽取出来，当做参数传递